Chapter 7: Evidence Evaluation and Scientific Progress

Scientists and philosophers of science share a concern for evidence evaluation and scientific progress. Their goals, however, are quite different. The philosophers find the process of science intrinsically interesting. Most are not trying to ‘straighten out’ the scientists and tell them how science should be done. Some of their conclusions do have possible implications for future scientific methods, but scientists seldom listen. Perhaps scientists’ reactions are somewhat analogous to those of creative writers toward literary critics and academic literary analysts: often the doer is unappreciative of the outside reviewer.

Each scientist unconsciously selects criteria for evaluating hypotheses. Yet clearly it would be both confusing and professionally hazardous to adopt substantially different criteria than those used by one’s peers. Judgment, not irrefutable evidence, is a foundation of science. Judgments that observations confirm or refute hypotheses are based on personal values: accuracy, simplicity, consistency, scope, progressiveness, utility, and expediency.

Different types of laws, or hypotheses, require different evaluation criteria [Carnap, 1966]. A universal law such as ‘all ravens are black’ is best tested by seeking a single exception. In contrast, a statistical law such as ‘almost all ravens are black’ or ‘99% of ravens are black’ requires a statistical test that compares observed frequencies to hypothesized frequencies. Theoretical and empirical hypotheses call for contrasting evaluation techniques and standards. For example, a theoretical-physics hypothesis may concern properties that are not directly measurable and that must be inferred indirectly, and it may be judged more on simplicity and scope than on accuracy of fit to observations.

This chapter considers all of these aspects of evidence evaluation.

*     *     *

Critical thinking skills and mistakes begun in childhood survive the transition to adult. Naive conceptions do not simply disappear when a more mature thinking skill is developed; they must be consciously recognized as wrong and deliberately replaced. For example, children learn about causality first by treating all predecessors as causal (“if I wear a raincoat and avoid getting wet, I won’t get a cold”). Only later and rather haphazardly is this superstitious approach supplanted by the skill of isolation of variables.

The most important childhood development in reasoning skill is obtaining conscious control over the interaction between theory and evidence [Kuhn et al., 1988]. Immature thinking fails to distinguish between theory and evidence. Scientific thinking requires critical evaluation of observations and of their impact on the validity of hypotheses. This skill is polished by practice -- particularly by coping with contradictory evidence and contradictory hypotheses.

In order to relate evidence to hypotheses effectively, the researcher needs three related skills [Kuhn et al., 1988]:

•     The evidence must be analyzed independently of the hypothesis, before evaluating the relationship between data and hypothesis.

•     One must be able to think about a hypothesis rather than just with it. If one allows the hypothesis to guide interpretation of the evidence, objective evidence evaluation is impossible.

•     While considering the impact of evidence on the hypothesis, one must be able to ignore personal opinion of the affected hypothesis. Favorable and unfavorable evidence must be given a chance to affect the final conclusion.

Kuhn et al. [1988] find that these three skills, which are absent in children and are developed gradually during middle adolescence and beyond, are still below optimum even in most adults.

Like most college students, I memorized facts and absorbed concepts, but I was seldom faced -- at least in class-work -- with the ‘inefficient’ task of personally evaluating evidence and deciding what to believe. Imagine my surprise when I went to graduate school, began reading the scientific literature, and discovered that even some ridiculous ideas have proponents. Textbook learning does not teach us the necessity of evaluating every conclusion personally -- regardless of how famous the writer is, regardless of how meager one’s own experience is.

Effective evidence evaluation requires active critical thinking, not passive acceptance of someone else’s conclusion. The reader of a publication must become a reviewer who judges the evidence for and against the writer’s conclusion.

Effective evidence evaluation is far more comprehensive than discrimination of whether statements are correct. It also involves assessment of the scope and ambiguities of observations, generalizations, and deductions, as well as the recognition of implicit and explicit assumptions. Have all perspectives been considered? Is any conclusion warranted by the evidence?

The evaluation techniques of this chapter can aid in this wresting of control from subconscious feelings and toward rational decision-making.

*     *     *

Judgment Values

Evidence evaluation, like scientific research in general, involves not only technique but also style. One’s judgment of an hypothesis or evidence set is more a product of subjective values than of objective weighting factors. Those values, like scientific research style, are based on personal taste.

Prediction of observations is perhaps the most compelling type of confirmation or refutation. As discussed later in this chapter, the confirmatory power of evidence depends on how surprising the prediction is. A rule of thumb is:

In forming a hypothesis, value minimum astonishment;
in testing hypothesis predictions, value maximum astonishment.

Thus hypotheses that are simple and, at least in hindsight, obvious are valued over convoluted ones. In contrast, the more unexpected and outlandish a prediction is, the more compelling it is if found to be correct. For example, Einstein was a master at forming theories that were based on the simplest of premises, yet yielded seemingly absurd but verifiably correct predictions.

Prediction is always valued over retrodiction, the ability of a hypothesis to account for data already known. This difference in values is because prediction constitutes an independent test of an idea, whereas existing data may have been incorporated in concept formation. For example, a polynomial may fit a set of time-series data excellently, yet generate bizarre predictions for regions outside the range of the input data. On shakier ground are retrodictions consisting of data that existed when the hypothesis was developed but of which the discoverer was unaware. The discoverer rightly considers them to be independent and successful predictions; the fact that the experiment preceded the hypothesis is irrelevant. The reviewer, however, cannot know whether or not the idea’s author was indirectly influenced by these data.

Comparison of a hypothesis to existing data is the first step in its testing, but this evaluation could have a hidden bias. The experiments were not designed specifically to test this hypothesis, so one must subjectively select ‘appropriate’ experiments and interpret departures from ideal experimental design. Predictions, in contrast, minimize these problems.

*     *     *

All scientists accept that hypothesis generation is subjective, but most cling to the myth that their evaluations of evidence are objective. Yet in recent decades the illusion of totally rational decision-making has collided with the technical difficulty of developing artificial intelligence (AI) programs. The successes and failures of AI suggest the scope of the problem. AI achieved rapid success in medical diagnosis, where each of an enormous number of potential symptoms has established statistical implications for potential diagnoses. In contrast, AI has progressed surprisingly slowly, in spite of great effort, in duplicating human language. Apparently, the ‘rules’ of grammar and ‘definitions’ of words are fuzzier and more qualitative than we had thought.

AI undoubtedly will expand dramatically during the next two decades, but its start has been sluggish, probably because of the subjectivity implicit in much scientific decision-making. “Every individual choice between competing theories depends on a mixture of objective and subjective factors, or of shared and individual criteria” [Kuhn, 1977]. These scientific decisions involve the weighing of competing advantages that are really not comparable or weighable. And even if one could develop a set of such weighting factors, we would find that they differ among individuals.

To identify these subjective weighting factors used in evidence evaluation, Kuhn [1977] asked “What are the characteristics of a good theory?” He identified five: accuracy, consistency, scope, simplicity, and fruitfulness. I add two others: utility and expediency. These are the seven main values on which we base our judgments concerning confirmation or refutation of hypotheses.

Accuracy -- and especially quantitative accuracy -- is the king of scientific values. Accuracy is the closest of the seven to an objective and compelling criterion. Accuracy is the value that is most closely linked to explanatory ability and prediction; hypotheses must accord with observations. Indeed, 2500 years after Pythagoras’ fantasy of a mathematical description of nature, quantitative accuracy is now the standard of excellence in all sciences that are capable of pragmatically embracing it.

The value placed on quantitative accuracy extends beyond the judging of hypotheses; it can affect one’s choice of scientific field. Highly quantitative sciences are not intrinsically superior to nonquantitative sciences; individual tastes are not comparable.

Simplicity is a value that is implicit to the scientist’s objective of identifying patterns, rules, and functional similarity among unique individual events. Yet all hypotheses seek order amid apparent complexity, so how does one apply the criterion of simplicity? William of Occam, a 14th-century English philosopher, developed ‘Occam's Razor’ as a method of cutting to the truth of a matter: “The simplest answer is the one most likely to be correct.” Also known as the maxim of parsimony, Occam’s Razor is an imperfect rule of thumb, but often it does select correctly among hypotheses that attempt to account for the same observations. The ‘simplest answer’ is not necessarily the one most easily comprehended. Often it is the one with the fewest assumptions, rationalizations, and particularly special cases, or it is the most elegant idea.

Sherlock Holmes countered the emphasis on simplicity by saying, “When all other contingencies fail, whatever remains, however improbable, must be the truth” [Doyle, 1917]. Yet when scientists resort to hypothesizing the improbable, they usually discover the actual truth later, among options that had been overlooked.

I still remember a sign that I saw on a restroom paper-towel dispenser twenty years ago: “Why use two when one will do?” The advice is in accord with Occam’s Razor: two or more hypotheses, each of which explains part of the observations, are less likely to be correct that one umbrella hypothesis that accounts for all of the data. Similarly, if an explanation becomes more and more complex as it is modified to account for incompatible observations, it becomes more suspect according to Occam’s Razor.

Complexity can result, however, from the interactions among two or more simple phenomena. For example, simple fractal geometric rules of repetition, when applied at different scales, can result in apparently complex patterns such as branching river systems and branching trees. Molecular biologists have long puzzled over how simple amino acids made the evolutionary leap to complex DNA; now these researchers are exploring the possibility that a few simple rules may be responsible [Gleick, 1992c].

The value on simplicity leads most scientists to be distrustful of coincidences. We recognize that they occur, but we suspect that most mask simple relationships.

Not everyone values simplicity similarly. Georg Ohm, a mathematics professor in Cologne, proposed in 1827 that electrical current in a wire is simply proportional to the potential difference between the wire ends. His colleagues considered this idea to be simplistic, and he was forced to resign his position. Eventually, his hypothesis was accepted and he resumed his academic career -- this time as professor of experimental physics. Today Ohm’s Law, which says that potential difference equals the product of current and resistance (in ohms), is the most useful equation in electricity.

Consistency, an aspect of simplicity, is valued in all sciences. The hypothesis should be consistent with relevant concepts that have already been accepted, or else it will face the formidable hurdle of either overthrowing the established wisdom or uneasily coexisting with incompatible hypotheses. Such coexistence is rare; one example is the physics concept of complementarity, discussed later in this section. An explanation must also be self-consistent: for example, all hypotheses are wrong, including this one.

In 320 B.C., Pytheas of Massilia sailed beyond the northernmost limits of the known world, to the land of Thule north of Britain. When he returned, he claimed that in Thule the midsummer sun did not set. His contemporaries called this observation preposterous.

Scope is another aspect of simplicity. A hypothesis that only accounts for the observations that inspired it has little value. In contrast, a hypothesis with a broad explanatory power inspires confidence through its ability to find order in formerly disparate types of observations. Scope is the antidote to Popper’s [1963] criticism that many similar confirmations can only marginally increase confidence in a hypothesis. A hypothesis with broad scope tends to be more amenable to diversified testing.

Progressiveness, or fruitfulness, is a seldom discussed value. Kuhn [1977] says simply that “a theory should be fruitful of new research findings: It should, that is, disclose new phenomena or previously unnoted relationships among those already known.” Most hypotheses seek to disclose previously unnoted relationships. Yet some are dead ends, sparking no further research except the confirmation or refutation of that specific conjecture. In contrast, progressive hypotheses are valued because of their exciting implications for a variety of new research directions. Even if a fruitful idea is later determined to be wrong, it can constructively steer future research efforts. Oliver [1991] thinks that the best criterion for the value of a scientific publication is the “impacts of the paper on the flow of science,” the extent to which it changes what other scientists do.

“A great discovery is a fact whose appearance in science gives rise to shining ideas, whose light dispels many obscurities and shows us new paths.” [Bernard, 1865]

“A great discovery is not a terminus, but an avenue leading to regions hitherto unknown. We climb to the top of the peak and find that it reveals to us another higher than any we have yet seen, and so it goes on.” [Thomson, 1961]

Utility is not just a crucial value for applied scientists; it is a common concern of all scientists. We scan journals and focus almost exclusively on articles that may be of some utility to us. To results that are not personally useful, we apply the most lethal hypothesis-evaluation technique: we ignore them. Similarly, the depth of our evaluation depends on the perceived relevance and utility of the hypothesis. When choosing between two hypotheses, we normally select the more pragmatic and useful one. For example, a useful empirical equation is often preferred over a rigorous theoretical equation, if the latter includes several variables that we are unable to estimate.

Expediency is concern for what is immediately advantageous, and scientific expediency favors acceptance of promised solutions to worrisome problems. Scientific anxiety is created when a ruling theory is threatened, or indeed whenever a discipline is faced with an apparently irreconcilable conflict -- perhaps between two incompatible hypotheses or perhaps between a strong hypothesis and a compelling dataset. Any evidence or ancillary explanation that promises remedy for the anxiety is likely to be received favorably -- almost gratefully -- because of the expediency factor. Valuing expediency can pose a pitfall, leading us beyond objective evidence evaluation and obscuring a broader question: how much do I want the idea to be confirmed, for other reasons?

*     *     *

Like all values, these seven are “effective guidance in the presence of conflict and equivocation” [Kuhn, 1977], not rigid criteria that dictate an unambiguous conclusion. “The criteria of choice … function not as rules, which determine choice, but as values, which influence it.” Like all values, these differ among individuals. Thus the disagreements between scientists about a hypothesis do not imply that one has misinterpreted data or made an error. More likely, they employ different subjective weightings of conflicting evidence. In Chapter 6, I argued that such disagreements are actually scientifically healthy and that they are an efficient means for advancing science; group objectivity grows from individuals’ subjectivity.

Scientific values differ between fields, and they may evolve within a field. For example, engineers and applied scientists emphasize the value of social utility as a key evaluation criterion, and they differ with physicists concerning the relative value of fruitfulness and simplicity. Kuhn [1977] notes that quantitative accuracy has become an evaluation criterion for different sciences at different times: it was achievable and valued by astronomy many centuries ago; it reached mechanics three centuries ago, chemistry two centuries ago, and biology in this century.

Like all human values and unlike rules, the scientific values are implicitly imprecise and often contradictory. For example, more complex hypotheses are usually more accurate than simple ones, and hypotheses with a narrow scope tend to be more accurate than those with a broad scope. Even a single value such as accuracy may have contradictory implications: a hypothesis may be more accurate than a competing idea in one respect and less accurate in another, and the scientist must decide which is more diagnostic.

An extreme example of the conflict between values is the quantum mechanics concept of complementarity, which achieves utility and expediency by abandoning consistency. According to complementarity, no single theory can account for all aspects of quantum mechanics. Concepts such as light as waves and light as particles are complementary. Similarly, the concepts of determining position precisely and determining momentum precisely are complementary. Furthermore, the concept of determining location in space-time is complementary to the concept of determinacy. In each case the pair of concepts is apparently contradictory; assuming one seems to exclude the other in an individual experiment. But full ‘explanation’ requires both concepts to be embraced, each in different situations. Complementary concepts only seem to be contradictory, because our perceptions are unable to reconcile the contradictions. The actual physical universe, independent of our observing process, has no such contradictions.

*     *     *

Evaluation Aids

Scientific progress depends on proper appraisal of evidence, on successful rejection of incorrect hypotheses and adoption of correct (or at least useful) hypotheses. Yet the evaluation techniques employed most often are incredibly haphazard, leading to conclusions such as ‘sounds reasonable’ or ‘seems rather dubious’.

 Evaluation of evidence is a scientific skill, perhaps the most important ability of a successful scientist. Like any skill, its techniques must be practiced deliberately and systematically, before one can trust its subconscious or casual use. For those who are mastering evidence evaluation, and even occasionally for experienced scientists, evaluation aids are useful. Here we describe three such techniques: model/observation tables, outlines, and concept maps.

*     *     *

A model/observation table succinctly compares several competing hypotheses. Usually various observations are relevant, with some favoring one idea while others favor another. Ideally, the scientist would examine each hypothesis systematically, reject those refuted by one or more evidence sets, and conclude that only a single hypothesis survives unscathed. In practice, we generally must weigh many inconclusive and partially contradictory data. The challenge to the scientist is to consider simultaneously this variety of evidence; a model/observation table is one way.

The model/observation table is a specialized and somewhat qualitative version of a truth table: list the models (or hypotheses) horizontally, list the relevant observations vertically, and then symbolically summarize the consistency of each observation with each model. Select symbols that are readily translatable into position along the continuum from strong confirmation to strong refutation:

+:   strong confirmation
+:   weak or ambiguous confirmation
0:   not relevant, or no data available
(alternatively, use a blank if ‘0’ implies ‘no’ to you)
-: weak or ambiguous refutation
--: strong refutation.

Table 11. Example of a model/observation table.

Observation	[A, '75]	[B&C, '76]	[D, '80]	[D&E, '81]
x/y correlation	+	-	+	+
y=3.7x	+	-	+	+
no y/z correlation	--	+	+	+
w= 5.2	0	0	+	+
x<w	+	+	+	+

For example, Table 11 summarizes the consistency of four published models with a group of five experimental findings. A quick scan of this table permits us to see that the leading hypotheses are those of D [1980] and of D & E [1981]; the latter is somewhat more successful but not decisively so. The hypothesis of A [1975], though consistent with many observations, is refuted by the observation of no y/z correlation. The hypothesis of B&C [1976] has mixed and unimpressive consistency with the observations. This quick overview allows identification of which observations are the most useful and consequently warrant the most careful attention. For example, the observation that x<w obviously is of no help in distinguishing among the possibilities.

The model/observation table is an easy way to focus one’s attention onto the most diagnostic relationships among observations and hypotheses. It counteracts the universal tendency toward letting one relationship dominate one’s thoughts. It encourages systematic evaluation of all relevant types of evidence. The table is not meant to be a simple tabulation of consistency scores, resulting in a bottom line success/failure score for each hypothesis. It cannot be that quantitatively objective, for the various observations are of unequal reliability and significance, in ways not readily reducible to a +/- symbol. Nevertheless, even experienced scientists often are surprised at how effectively this underused technique can draw their attention to the crux of a problem.

An outline is a familiar technique that is readily adapted for evidence evaluation. An outline works effectively for analysis of one or two major hypotheses. For multiple hypotheses, it has considerable redundancy because different hypotheses are affected by the same arguments. In contrast, the model/observation table is more compact and is concentrated on identifying differences among hypotheses. Like the model/observation table, an outline permits both arguments for and arguments against a hypothesis. It also permits nested hypotheses: often the premise for one conclusion has its own premises, strengths, and weaknesses. An evidence-evaluation outline might look like the following:

I. Hypothesis

  A) argument for hypothesis

    1) primary confirmation of A

    2) secondary confirmation of A

    3) ambiguity

  B) strong argument for hypothesis

    1) primary confirmation of B

    2) secondary confirmation of B

    3) But evidence against B

       a) confirmation of #3

       b) But alternative explanation for #3

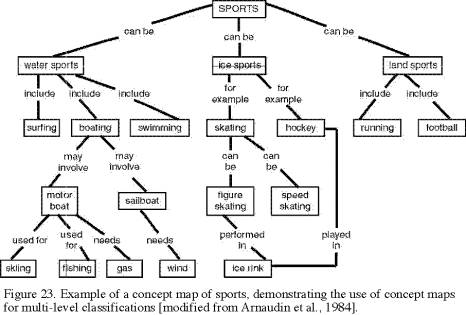
A less structured alternative to outlines and model/observation tables is the concept map, a flowchart that summarizes the known (or inferred) relationships among a suite of concepts. It is adaptable as a learning aid or as a method of evidence evaluation; at present it is used primarily as the former. Figure 23 illustrates the technique with a high-school-level concept map of sports [Arnaudin et al., 1984].

Concept mapping is based on a learning theory called cognitive association [Ausubel et al., 1978]. Cognitive association goes beyond the fixed patterns of simple memorization; like science, it evolves to encompass new knowledge. It employs the synergy of linking a new idea to existing ones: the new concept is easier to remember, and it subtly changes one’s perceptions of previously known ones. Additional ideas are subsumed into the existing conceptual framework and, like analogies, gain meaning from familiarity of patterns.

Based on teaching concept mapping to several hundred students, Arnaudin et al. [1984] reach the following conclusions about this technique:

• it is an effective study technique.

• it improves one’s ability to comprehend complex phenomena, by dissecting them into graspable components and links.

• it helps one to identify gaps in knowledge and understanding, thereby lending a goal-oriented aspect to further learning.

A scientific publication can be concept mapped with the following seven-step procedure, adapted from one developed by J. D. Novak [Arnaudin et al., 1984]:

1) read the publication, highlighting or underlining key ‘concepts’ as you go. ‘Concepts’ can be hypotheses, assumptions, equations, or experiments, but not relationships.

2) skim back through the publication, systematically highlighting previously overlooked concepts that seem relevant to the overall context.

3) transfer all of the highlighted concepts to a list. Try to list the most general ones near the top and the less inclusive, more specific ones near the bottom. Sometimes an entire suite of related concepts can be encompassed in a larger-scale box representing a packaged general theory.

4) transfer the list onto a concept ‘map’, where broad categories are placed near the top of the map and successively more restrictive categories are placed successively lower on the map. Place similar concepts or categories on the same level, grouping related ones. Draw lines linking concepts on different levels. Label each line with a simple linking word that identifies the relationship between the pair of ideas.

5) ‘branch out’, adding concepts and links that were not in the publication but are suggested by examination of the map.

6) create ‘cross-links’, identifying connections between concepts that may be more distant than the simple downward branching of the overall concept map. This cross-linking procedure may even suggest a radical redrawing of the map, thereby simplifying its structure.

7) highlight, or weight, key concepts and links with bold lines or boxes, and use dashed lines and question marks for suspect portions.

Am I insulting the reader by suggesting that a high-school or college learning technique such as in Figure 23 is also useful for the professional scientist? Long before the term concept mapping was invented, a very similar flowchart technique was used by scientists and other professionals, for the identical purpose of visualizing the relationships among complex phenomena. For example, Figure 24 [Bronowski, 1973] is a page from the notes of John von Neumann, one of the most outstanding mathematicians of the 20th century; apparently his photographic memory did not preclude the usefulness of conceptual flowcharts. Figures 4 and 22 are additional examples. For the scientist who is analyzing and evaluating a scientific article, or who is trying to work through a complex idea, concept mapping can be a visualization and evaluation aid.

*     *     *

Model/observation tables, outlines, and concept maps are quite different in format but similar in function. Each provides a visual structure that attempts to assure that all relevant information and relationships are considered, that focuses attention on pivotal concerns, and that identifies strengths and weaknesses. Popular memory aids such as underlining, note-taking, and paraphrasing do not fulfill these objectives as reliably.

The scientist who attempts to visualize the entire pattern of evidence risks neglecting a crucial relationship. Writing it in a systematized form may reveal that gap.

Because model/observation tables, outlines, and concept maps compel the scientist to organize knowledge, they are a wonderful first step toward writing up scientific results for publication.

*    *     *

Confirmation and Refutation of Hypotheses

The evaluation aids can organize a set of evidence effectively. The crux of evidence evaluation, however, is scientific judgment concerning the implications of datasets for hypotheses. Evaluation aids, like scientific progress, constantly demand this judgment: do the data confirm or refute the hypothesis?

Confirmation and verification are nearly synonymous terms, indicating an increase in confidence that a hypothesis is correct. Unfortunately, the terms confirmation and verification are widely misused as simple true/false discriminators, like prove and disprove. Rarely are experiments so diagnostic as to prove or disprove a hypothesis. More frequently, evidence yields a qualitative confirmation or its converse, refutation.  

It is often said (e.g., by Einstein, Popper, and many others) that no quantity of tests confirming a hypothesis is sufficient to prove that hypothesis, but only one test that refutes the hypothesis is sufficient to reject that hypothesis. This asymmetry is implicit to deductive logic. Two philosophical schools -- justificationism and falsificationism -- begin with this premise and end with very different proposals for how science ‘should’ treat confirmation and refutation of hypotheses.

*     *     *

The philosophical school called justificationism emphasizes a confirmation approach to hypothesis testing, as advocated by proponents such as Rudolf Carnap. Any successful prediction of an hypothesis constitutes a confirmation -- perhaps weak or perhaps strong. Each confirmation builds confidence. We should, of course, seek enough observations to escape the fallacy of hasty generalization.

Carnap [1966] recommended increasing the efficiency or information value of hypothesis testing, by making each experiment as different as possible from previous hypothesis tests. For example, he said that one can test the hypothesis “all metals are good conductors of electricity” much more effectively by testing many metals under varied conditions than by testing different samples of the same metal under rather similar conditions. This approach is analogous to the statistical technique of using a representative sample rather than a biased one, and its goal is the same: to assure that the properties exhibited by the sample are a reliable guide to behavior of the entire population.

Carnap seems to take this analogy seriously, for he argued that it is theoretically possible to express confirmation quantitatively, by applying a ‘logical probability’ to each of a suite of hypothesis tests and calculating a single ‘degree of confirmation’ that indicates the probability that a hypothesis is correct. Jeffrey [1985] proposed adoption of ‘probabilistic deduction’, the quantitative assessment of inductive arguments, based on calculating the odds that a hypothesis is correct both before and after considering a dataset.

Justificationism and probabilistic deduction have been abandoned by philosophers of science and ignored by scientists, for several reasons. The decision on how many observations are needed is, unfortunately, a subjective one dependent on the situation. The quest for heterogeneous experimental conditions is worthwhile, but it is subjective and theory-dependent. Even if we could confine all of our hypothesis tests to statistical ones with representative samples, we cannot know that the tests are representative of all possibly relevant ones. The confirming observations are fallible and theory-dependent; we look mainly for what the hypothesis tells us is relevant. Furthermore, we have no way of knowing whether a different hypothesis might be proposed that explains all of the results just as well. Thus we can infer from a large number of confirmations that a hypothesis is probably correct. We cannot, however, quantify this probability or even know that it is greater than 50%.

*     *     *

Karl Popper focused on these weaknesses of confirmation and concluded that additional ‘confirmations’ do not necessarily and substantially increase confidence in a hypothesis. In reaction, he created a philosophy for hypothesis testing known as falsificationism. Starting from the premise that the only compelling experiment is one that disproves a hypothesis, he argued that the task of science should be falsification, the rejection of false theories.

First proposed in 1920 and eloquently advocated by Popper, falsificationism had a substantial following among philosophers of science for several decades, and many aspects of it survive. Yet falsifiability has been virtually ignored by scientists. Popper’s vision of science is generation of a myriad of ideas followed by ruthless falsification and rejection of the majority. This vision does not correspond with the experience of scientists, but of course our subjective experience could be misleading.

Most scientists do agree that testability is a fundamental criterion for deciding which hypotheses are worthy of attention, but none agree with Popper’s assessment that falsifiability is supreme, nor that minor supporting roles are played by confirmation, discovery, insight, and subjective context-dependent evaluation. “An idea may be neither demonstrably true nor false, and yet be useful, interesting, and good exercise” [Trotter, 1941].  A concept may be embraced even without falsifiability, if it is capable of finding elegance of pattern among anomalous observations. Virtually the only mention of falsifiability that I have seen in my field (geology/geophysics) was Ken Hsü’s claim that Darwinian evolution is nonscientific because it is not falsifiable. Is the scientific method nonscientific, because its assumption of causality is neither provable nor disprovable?

Falsifiability is a tool, not a rule. The logical flaw in falsificationism is its deductive conclusion that a single inconsistent observation disproves a hypothesis. Scientists do not agree to follow this simple path for evaluating hypotheses, because the source of the inconsistency may be problems in the data, assumptions, or experimental conditions. Kuhn [1970], several other philosophers of science, and Wilson [1952] have cited numerous examples of theories surviving in spite of ‘falsifying observations’:

Newton’s laws exhibited incredible predictive value. Although they failed to account completely for planetary orbits, they were not rejected.

The chemical ‘law’ of Dulong and Petit is that the specific heat of each solid element multiplied by its atomic weight is approximately 2 calories per degree. This empirical relationship was used for many years, in spite of the early recognition that it did not work for either silicon or carbon. The exceptions were neither ignored nor used to reject the hypothesis. Ultimately they helped to guide establishment of a law more founded in theory. From the perspective of that new law, Dulong and Petit’s law was a special limiting case.

Copernicus’ 1543 proposal that the earth revolves around the sun initially conflicted with many observations. The ‘tower argument’ was particularly damning: if the earth really is spinning, then an object dropped from a tower should land west of the tower, not -- as observed -- at its foot. Fortunately the theory was not discarded.

*     *     *

Power of Evidence

The successful middle ground between avid justificationism and falsificationism is a concern with the power of evidence. Information is proportional to astonishment, or, in terms of information theory, the value of a piece of information is proportional to the improbability of that information.

The most powerful and therefore most useful experiment depends on the situation: it may be the experiment most likely to confirm, or to refute, a hypothesis. The fate of most novel, sweeping hypotheses is a quick death, so their refutation has little impact on science. Confirmation of such a hypothesis, on the other hand, does have substantial information value. Similarly, many hypotheses are only incremental modifications of previous theories and so their confirmations are expected to be pro forma. Refutation of such a hypothesis may force us to rethink and revise our core assumptions. Well established theories are not normally tested directly, but when such a theory is found to be irreconcilable with an apparently rigorous experiment, this powerful and informative anomaly fosters intensive analysis and experimentation.

Ronald Giere [e.g., 1983] is one of the leading proponents of the ‘testing paradigm’, more popularly known as the diagnostic experiment. A diagnostic experiment avoids the ambiguity of weak true/false tests such as those of justificationism and falsificationism, and it avoids qualitative value judgments. The diagnostic test is the key test, the scalpel that cuts to the heart of a hypothesis and yields a result of ‘true’ if the prediction is confirmed, and ‘false’ if the prediction is refuted.

For normal science, the diagnostic experiment is generally a myth -- an ideal to be sought but seldom achieved. The diagnostic experiment is, nevertheless, a worthy goal, for it is far better to fall short of the perfectly diagnostic experiment than to fire random volleys of experiments in the general direction of an hypothesis.

Jonas Salk [1990] has the ideal of a diagnostic experiment in mind when he says: “Solutions come through evolution. It comes from asking the right question. The solution preexists. It is the question that we have to discover.”

Clausewitz [1830] gives analogous advice to military planners: “A certain center of gravity, a center of power and movement, will form itself, on which everything depends… We may, therefore, establish it as a principle, that if we can conquer all our enemies by conquering one of them, the defeat of that one must be the aim of the War, because in that one we hit the common center of gravity of the whole War.”

*     *     *

The Raven’s Paradox [e.g., Lambert and Brittan, 1970; Mannoia, 1980] is an inductive problem that provides a surprising and useful perspective on the power of evidence. Suppose we wish to test this hypothesis: ‘All ravens are black.’ Symbolically, we can express this hypothesis as R⇒B (Raven implies Black) or ‘R, ∴B’ (Raven, therefore Black). Any example of a raven that is black provides confirmatory evidence for the validity of the hypothesis. Even one instance of a raven that is not black proves that the hypothesis is wrong.

The paradox arises when we consider the implications of the following rule of logic: each statement has logically equivalent statements (Chapter 4), and if a statement is true, its logically equivalent statement must also be true. A logical equivalent of the hypothesis ‘All ravens are black’ is ‘All non-black things are not ravens.’ Caution (or practice) is needed to be certain that one is correctly stating the logical equivalent. ‘All non-ravens are not black’ superficially sounds equivalent to ‘All ravens are black,’ but it is not.

The Raven’s Paradox is this: anything that is both not black and not a raven helps confirm the statement that all ravens are black. Without ever seeing a raven, we can gather massive amounts of evidence that all ravens are black.

The Raven’s Paradox has been the subject of much discussion among philosophers of science. Some of this discussion has concluded that seemingly absurd types of evidence (not-Black + not-Raven confirms R⇒B) are nevertheless valid, but most arguments have centered on the intrinsic weakness of the confirmation process. In contrast, I see the tests of the Raven’s Paradox, like all scientific evidence, in terms of information value. Observations of non-ravens do help confirm the hypothesis that ‘All ravens are black,’ but the information value or evidential power of each observation of a non-raven is miniscule. Even thousands of such observations are less useful than a single observation of a raven’s color. Were this not so, we could use the concept of logical equivalence to ‘confirm’ more outrageous hypotheses such as ‘All dragons are fierce.’

Like the example in Chapter 3 of the ‘cause’ of Archimedes’ death, many inferences form a pattern: X₁⇒X₂⇒X₃⇒X₄. All elements of the pattern are essential; all elements are not of equal interest. Familiar relationships warrant only peripheral mention. The pattern link of greatest scientific interest is the link that has the maximum information value: the most unusual segment of the pattern.

*     *     *

Scientific research is intimately concerned with the power of evidence. Inefficient scientists are transient scientists. The demand for efficiency requires that each researcher seek out the most powerful types of evidence, not the most readily available data. In the case of the Raven’s Paradox, this emphasis on experimental power means first that only ravens will be examined. Furthermore, a single instance of a non-black raven is much more important than many instances of black ravens, so the efficient scientist might design an experiment to optimize the chance of finding a non-black raven. For example, the hypothesis ‘All dogs have hair’ could be tested by visiting several nearby kennels, but a single visit to a Mexican kennel, after some background research, might reveal several examples of Mexican hairless dogs.

To the logician, a single non-black raven disproves ‘All ravens are black’, and a single Mexican hairless disproves ‘All dogs have hair.’ The scientist accepts this deductive conclusion but also considers the total amount of information value. If exceptions to the hypothesis are rare, then the scientist may still consider the hypothesis to be useful and may modify it: ‘99.9% of ravens are black and 0.1% have non-black stains on some feathers,’ and ‘All dogs except Mexican hairlesses have hair.’

*     *     *

Hypothesis Modification

The distinction between scientists’ and logicians’ approaches does not, of course, mean that the scientist is illogical. Confirmation and refutation of hypotheses are essential to both groups. They usually do not, however, lead simply to approval or discarding of scientific hypotheses. In part, this outcome is progressive: the hypothesis as originally stated may be discarded, but the scientific companion of refutation is modification. In many cases, simple acceptance or rejection is not possible, because hypotheses are usually imperfect.

Confirmation or falsification of a hypothesis, like the ‘diagnostic experiment’, can be difficult to achieve, for several reasons:

• Many hypotheses have inherent ambiguities that prevent simple confirmation or falsification. An experiment may favor one interpretation of a hypothesis, but the door is left open for other interpretations.

• Most experiments, in spite of careful experimental design, have at least some inherent ambiguity.

• Most hypotheses and their tests have associated assumptions and concepts. Refuting evidence indicates inadequacy of either the main hypothesis or corollaries, and one may not know confidently which to reject. Typically, the ‘hard core’ of a theory is relatively invulnerable to attack, and we refute or modify the ‘protective belt’ of ancillary hypotheses, assumptions, and conditions [Lakatos, 1970].

• Instead of directly testing a hypothesis, we usually test deductive or inductive predictions derived from the hypothesis. This prediction may be wrong rather than the hypothesis.

Proof or disproof of a hypothesis is often impossible; rarely, search for proof or disproof can be undesirable. Frequently the scientific community loses interest in endless tests of a hypothesis that is already judged to be quite successful; they change the focus to characterization of the phenomenon. Then inductive predictions are the target of experiments, because little ambiguity remains about whether one is testing the hypothesis or its inferred implications. Symbolically, if h is a hypothesis, p_i is an inductive prediction, and p_d is a deductive prediction, then some possible hypothesis tests are:

h, directly testable;

h⇒p_d, p_d testable so h testable;

h⇒p_i, p_i testable but h is not directly tested.

A school of thought known as conventionalism recognizes the networked nature of most hypotheses and the associated ambiguity of most confirmation/refutation evidence, as well as the seductiveness of modifying an otherwise successful hypothesis to account for inconsistent observations. Conventionalists conclude that subjective judgment is required in evaluating hypotheses, and they suggest that values such as simplicity and scope are used in making these judgments.

If the conventionalists are correct about how science works, then the subjectivity of evidence evaluation is a major obstacle to our quest for reliable knowledge. The weakness of conventionalism is its fluidity. Two scientists can examine the same evidence and embrace opposing views, because of different criteria for evidence evaluation. Most hypotheses are wrong, but demonstration of their errors leads more often to a modification of the hypothesis than to its rejection. This band-aid approach, though powerful and often successful, can lead the researcher into evaluating how reasonable each slight modification is, without detecting how cumbersome and unreasonable the composite hypothesis has become. Unless one holds tightly to the criterion of simplicity, there is the danger that any wrong hypothesis will stay alive by cancerously becoming more and more bizarre and convoluted to account for each successive bit of inconsistent data.

When Galileo aimed his telescope at the moon and described mountains and craters, his observations conflicted with Aristotelian cosmology, which claimed that all celestial objects are perfect spheres. A defender of the old view had this ad hoc explanation: an invisible, undetectable substance fills the craters and extends to the top of the mountains.

Imre Lakatos [1970] attempted to put a brake on this unconstrained ad hoc hypothesis modification by imposing a standard: if a hypothesis is modified to account for a conflicting observation, then it must not only account for all previous results just as well as did the original hypothesis, but also make at least one new and successful prediction.

Lakatos’ goal is worthwhile: steering the evolution of hypotheses toward those that have greater explanatory power. His method is feasible, if a bit awkward. Usually the hypothesis revision occurs after a project has obtained its research results, so the actual test of the new prediction is deferred for a later paper by the same or different authors. Lakatos’ criterion is virtually unknown and unused among scientists, however. Its problem is the same as that of falsificationism: it is an outside judgment of what scientists should do (according to the proponent), rather than a description of what they actually do, and we scientists are not persuaded of the need to change. We can, however, be alert for ad hoc hypotheses, and we do expect a modified hypothesis to explain more than its predecessor.

I and many other scientists are close to this conventionalist view. We are, perhaps, even closer to Thomas Kuhn’s perspective, described in the next section.

*     *     *

Paradigm and Scientific Revolution

Thomas Kuhn’s 1963 (and 1970) book The Structure of Scientific Revolutions overthrew our perception of scientific change. We had imagined scientific change as a gradual process, involving incremental advancement in techniques, evidence, and hypotheses, which resulted in a steady increase in scientific knowledge.

Our textbooks reinforced this view by portraying the history of scientific thought from our present perspective. Early ideas are judged to be important and relevant only to the extent that they contribute to the continuous evolution toward the current ideas. Textbooks express the outcomes of scientific revolutions as discoveries of new ideas; they avoid confusing this picture with discussion of the process of scientific upheavals and of the ideas that have been superseded. Because most science students read textbooks rather than scientific articles prior to initiating their own graduate research, their perception of scientific change is fossilized even before they have a chance to contribute to that change.

Kuhn said that we must consider scientific results in the context of the sociological factors and scientific perspectives of their time. He saw the advance of science more as a staircase than a ramp. Within each scientific field, long periods of stability and consolidation are followed by short periods of major conceptual revision, or paradigm change. I think that this view of science is progressive: not only is it a more realistic perspective, but also it offers insights into which scientific methods are most appropriate at different points in the evolution of a science.

A paradigm is a suite of “universally recognized scientific achievements that for a time provide model problems and solutions to a community of practitioners” [Kuhn, 1970]. Kuhn realized that this definition is vague and sloppy. To me, a paradigm is a coherent suite of theories or concepts that guide interpretations, choice of relevant experiments, and development of additional theories in a field or discipline. Physics paradigms, for example, included Newtonian dynamics, general relativity, and quantum mechanics.

We can understand paradigms better by considering a field in its pre-paradigm state. Data collection is unfocused, a fishing expedition rather than a hunter’s selection of prey. Facts are plentiful, but the overall patterns and organizing principles are unclear. Several schools of thought compete, none agreeing on what phenomena warrant study and none providing broad-scope hypotheses. Research is overwhelmed by the apparent complexity of the subject.

*    *     *

When a paradigm guides a scientific field, nearly all research is considered in relation to that paradigm. Research is focused; the paradigm indicates which research topics are appropriate and worthwhile. Both theoretical and experimental studies are largely confined to three foci:

1) collecting data to test predictions of the paradigm;

2) pursuing aspects that may elucidate seminal phenomena. These investigations often require development of more sophisticated, more accurate equipment; and

3) attempts to ‘articulate’ the paradigm, including efforts to extend it and account for other phenomena, and attempts to resolve apparent problems or ambiguities.

Paradigm change is rare; working under a guiding paradigm is the norm. These ‘mopping-up operations’ are exciting because they promise goal-oriented, steady progress rather than a frustrating floundering. Often the results of experiments are readily predictable, but the work is still challenging. Ingenuity and insight are needed to determine how to conduct the experiment most successfully and elegantly.

*     *     *

Researchers ignore most data that appear to be unrelated to or unexplained by the paradigm. Moreover, we tend to ignore evidence that conflicts with the paradigm. No paradigm explains all observations, because no paradigm provides ultimate and final truth. Yet the immense explanatory power of the paradigm leads scientists to think of the contradictory data either as mistaken or as explicable by future elaborations of the paradigm. In either case, the results can be ignored for the moment -- or so we tell ourselves, if we even notice the contradictions. Publication of evidence that seems to conflict with the paradigm is hazardous, for the authors risk being branded as nonbelievers or outsiders.

An established paradigm is insulated from overthrow, by both the tendency to ignore discrepant facts and by the habit of refining hypotheses and paradigms [Kuhn, 1970]. Even when many anomalies are found, we do not discard the paradigm, for rejection leaves a vacuum. Rejection implies that all the predictive successes of the paradigm were coincidental. Only when a new potential paradigm appears will abandonment of the old be considered. Scientific inertia is conservative: a new paradigm is accepted only if it is demonstrably superior -- not merely equal in success -- to the old paradigm.

Timing of the new paradigm’s appearance is critical. It must be considered when anxiety over anomalies in the old paradigm is high. Without the leverage of anomaly anxiety, attempts to challenge the paradigm’s authority are likely to fail (e.g., Plato vs. democracy, Aristotle vs. slavery, Descartes vs. experimental science, and Einstein vs. quantum mechanics). Introduction of a new theory too early will encounter complacency with the old one. Indeed, sometimes the new paradigm is a reintroduction and slight refinement of a previously proposed idea, which had failed to gain momentum.

Discovery “commences with the awareness of anomaly (i.e., with the recognition that nature has somehow violated the paradigm-induced expectations), continues with extended exploration of the area of anomaly, [and] concludes when the paradigm has been adjusted so that the anomalous has become the expected.” [Kuhn, 1970]

*     *     *

Paradigm change begins with a single anomaly that cannot be ignored. Anomaly creates a sense of trauma or crisis, as we saw in the card-flashing experiment [Bruner and Postman, 1949] when the subject said, “I’m not even sure now what a spade looks like. My God!” The sense of crisis and anxiety grows with recognition of the many smaller anomalies that had been overlooked. The entire foundation of the field seems unstable, and doubts arise about the value of familiar paradigm-inspired experiments.

Anxiety creates a willingness, even a need, to consider alternative paradigms. The field splits into two camps: that which suggests competing piecemeal solutions to the various anomalies, clinging to the old paradigm, and that which considers alternative paradigms. This second group of investigators refuses to accept rationalizations of the major anomaly. These scientists explore the anomaly more deeply and attempt to characterize it, simultaneously looking for invalid assumptions.

“That is in the end the only kind of courage that is required of us: the courage to face the strangest, most unusual, most inexplicable experiences that can meet us.” [Rilke, 1875-1926]

Reconciliation of the problems seldom comes rapidly. The period of paradigm crisis can last for years or decades, and anxiety may become discouragement. Perhaps the new paradigm will require new technology and its attendant new insights. Almost always, the new paradigm is discovered by someone young or new to the field, someone less hampered than most by perspectives and assumptions of the old paradigm. The new paradigm may be a radical modification of the old paradigm. The old paradigm may be seen as a special limiting case of the new one, as was the case for Newtonian dynamics when seen from the perspective of Einstein’s dynamics.

Paradigm change may be led by a few people, but usually it involves many people working over a period of several years. Within the subgroup that had been bothered by the anomalies, a consensus of both experimenters and theoreticians emerges, concerning the advantages of a new paradigm over the old one. Simultaneous independent discoveries are likely. Now is the most exciting time, with the (mostly young) proponents of the new paradigm exploring the range of its applications. The pace of change is extremely fast: only those who are attending conferences, receiving preprints, and learning the new jargon are fully aware of these changes.

Polarization of old and new schools continues well beyond the acceptance by the majority of the new paradigm. The old and new paradigms identify different subjects as appropriate for research and emphasize controlling different variables. Communication between the two schools breaks down. Neither paradigm accounts for every observation; thus each group can point to anomalies or weaknesses in the other paradigm. But with time the demand of the new majority is fulfilled: “convert or be ignored” [Kuhn, 1970].

*     *     *

These interpretations of the pattern of change in science are those of Thomas Kuhn; they are not accepted universally. Stephen Toulmin [1967] suggested that scientific change is more evolutionary than Kuhn has pictured it. Toulmin used the analogy of biological evolution, emphasizing that competing theories abound, and the more successful ones eventually triumph. The analogy was unfortunate, for most paleontologists now see evolution as dominantly episodic or revolutionary -- a punctuated equilibrium [Eldredge and Gould, 1972].

Scientific change is punctuated illumination. For both scientific and biological evolution, relatively stable periods alternate with periods of dynamic change, but no one suggests that the stabler times are stagnant. Mannoia [1980] summarized the philosophical trend of the seventies as moving away from the Kuhn/Toulmin perspectives, toward an ‘historical realism’, but I think that the jury is still out.

Few books in philosophy of science have attracted the interest of scientists; Kuhn’s [1970] book is an exception. His vision of scientific change -- continuous incremental science, plus rare revolution -- is fascinating to those in fields undergoing this punctuated illumination. The changes associated with the 1968 geological paradigm of plate tectonics appear to fit his model, as does the recent paradigm of chaos, described by Gleick [1987] as a “revolution in physical sciences”. Successful prediction always confirms a model more persuasively than does detection of apparent pattern within existing data.

*     *     *

“Yet when we see how shaky were the ostensible foundations on which Einstein built his theory [of general relativity], we can only marvel at the intuition that guided him to his masterpiece. Such intuition is the essence of genius. Were not the foundations of Newton’s theory also shaky? And does this lessen his achievement? And did not Maxwell build on a wild mechanical model that he himself found unbelievable? By a sort of divination genius knows from the start in a nebulous way the goal toward which it must strive. In the painful journey through uncharted country it bolsters its confidence by plausible arguments that serve a Freudian rather than a logical purpose. These arguments do not have to be sound so long as they serve the irrational, clairvoyant, subconscious drive that is really in command. Indeed, we should not expect them to be sound in the sterile logical sense, since a man creating a scientific revolution has to build on the very ideas that he is in the process of replacing.” [Hoffmann, 1972]

*     *     *

Pitfalls of Evidence Evaluation

Scientific progress under a guiding paradigm is exhilarating. Paradigm-driven science can, however, undermine the objectivity with which we evaluate hypotheses and evidence.

Hidden Influence of Prior Theory on Evidence Evaluation

Data evaluation should consist of three separate steps: (1) objective appraisal of the observations, (2) confirmation or refutation of a hypothesis by these data, and (3) overall evaluation of a hypothesis in the context of these and other observations. All too often, we allow our prior opinion of a hypothesis to influence the evaluation of new evidence (steps #1 & 2), without being aware of the bias. This hidden influence is a pitfall, whereas it is completely valid to weight prior evidence more than the new data (step #3). In both cases, the impact of evidence depends on the perceived strength of the hypothesis it affects. Evidence sufficient to uproot a weakly established hypothesis may fail to dislodge a well established one.

We value simplicity, and it is much simpler and more comfortable if new evidence confirms previous beliefs than if it creates conflict. Ideally, one (and only one) hypothesis is consistent with all observations. To obtain this ideal, we may subconsciously reject evidence that conflicts with the hypothesis, while overemphasizing evidence that supports it. We must beware this subconscious theory-based rejection of data.

Children and adults use similar strategies to cope with evidence that is inconsistent with their prior beliefs [Kuhn et al., 1988]:

• consciously recognize the discrepancy and conclude that either the hypothesis or the evidence is wrong;

• consciously recognize the discrepancy, then deliberately revise the hypothesis to make it more compatible with the evidence;

• reduce the inconsistency by biased interpretation of the evidence;

• subconsciously revise the hypothesis to make it more compatible with the evidence.

All four strategies also are employed by scientists, but only the first two are valid. The first three have been discussed already and are also familiar in daily experience. Subconscious revision of a hypothesis, in contrast, is a surprising pitfall. Kuhn et al. [1988] found that subjects usually modified the hypothesis before consciously recognizing the relationship of the evidence to the hypothesis. They seldom realized that they were changing the hypothesis, so they failed to notice when their theory modification was implausible and created more problems than it solved. Fortunately for science but unfortunately for the scientist who succumbs to the pitfall of subconscious hypothesis modification, someone usually detects the error.

Kuhn et al. [1988] found that hypotheses of causal relationships between variables are particularly resistant to overthrow by new data. The new data must overcome the expectation of a correlation; even if the data set as a whole does so, nonrepresentative subsets may still appear to confirm the correlation. Furthermore, the original proposal of a causal relationship probably also included a plausible explanation. To discard the correlation is also to reject this explanation, but the new data do not even address that argument directly.

The hidden influence of accepted hypotheses on evidence evaluation harms scientists as well as science. A scientist’s beliefs may fossilize, leading to gradual decrease in creative output (though not in productivity) throughout a professional career.

As we saw in the previous section on paradigms, hidden influence of prior theory has other manifestations: (1) ignoring data inconsistent with the dominant paradigm; (2) persistence of theories in spite of disproof by data; and (3) failure to test long-held theories.

*     *     *

Incremental Hypotheses and Discoveries

Because the dominant paradigm molds one’s concepts, it largely controls one’s expectations. Hypotheses and discoveries, therefore, tend to be incremental changes and elaborations of the existing theories, rather than revolutionary new perspectives. Mannoia [1980] says that “the answers one obtains are shaped by the questions one asks.”

*     *     *

‘Fight or Flight’ Reaction to New Ideas

The expression ‘fight or flight’ describes the instinctive reaction of many animal species to anything new and therefore potentially threatening. Beveridge [1955] pointed out that ‘fight or flight’ is also a scientific pitfall. When presented with new ideas, some individuals fight: the theory is immediately rejected, and they only listen to pick out flaws. Their biased attitude should not be confused with the scientifically healthy demand, ‘show me’, suspending judgment until the evidence is heard. Other scientists flee, ignoring any new idea until more conclusive, confirming evidence can be provided. A scientist who rejects relevant evidence, on the grounds that it leaves questions unanswered or it fails to deliver a complete explanation, is confusing the responsibilities of evidence and hypothesis.

“The mind likes a strange idea as little as the body likes a strange protein, and resists it with a similar energy… If we watch ourselves honestly we shall often find that we have begun to argue against a new idea even before it has been completely stated.” [Trotter, 1941]

“In the 1790’s, philosophers and scientists were aware of many allegations of stones falling from the sky, but the most eminent scientists were skeptical. The first great advance came in 1794, when a German lawyer and physicist, E.F.F. Chladni, published a study of some alleged meteorites… Chladni’s ideas were widely rejected, not because they were ill conceived, for he had been able to collect good evidence, but because his contemporaries simply were loathe to accept the idea that extraterrestrial stones could fall from the sky.” [Hartmann, 1983]

*     *     *

Confusing the Package and Product

Scientists are not immune to the quality of the sales pitch for a set of evidence. Unless the reader is put off by blatant hype, the sales pitch exerts a subconscious influence on one’s evaluation of the evidence. For example, consider the statement “All hypotheses are wrong, but some are more wrong than others.” Catchy expressions tend to go through one’s head and thereby gain strength, while qualifications and supporting information are forgotten. In this one a defeatist mood is enforced, rather than the optimistic prospect of growth and evolution of changing ideas. To separate the objective evidence from the effects of presentation style, paraphrasing arguments can help.

*     *     *

Pitfall Examples

For over 2000 years, from the ancient Egyptian, Greek, Roman, Chinese, and Japanese cultures to the 19th century, there persisted the myth of the oxen-born bees. The myth, ‘confirmed’ by observation, explained that decaying carcasses of oxen transformed into a swarm of honeybees.

The birth that people witnessed so often was not of honeybees but rather of the fly Eristalis tenax, which looks similar. The flies do not generate spontaneously; they hatch from eggs laid in the carcasses. In all that time, though people had seen developing honeybees in honeycombs, no one captured the oxen-born bees and attempted to raise them for honey, nor did they compare them with honeybees, nor did they observe the egg laying or the eggs [Teale, 1959].

Pitfalls: failure to test long-held theories;
missing the unexpected;
missing important ‘background’ characteristics.

In 1887, physicist Albert Michelson and chemist E.W. Morley carried out an experiment to detect the earth’s motion through the ether. They measured the difference in the travel times of light moving at different angles to the earth’s presumed direction through the ether. Although theory indicated that the measurements were sensitive enough to detect this effect, the Michelson-Morley experiment found no difference. Fortunately for physics, these scientists did not suppress their negative results. They published, although for 15 years Michelson considered the experiment a failure [Hoffmann, 1972]. Theories assuming the existence of an ether survived the emergence of this and other anomalies, until Einstein’s 1905 paper on special relativity changed the paradigm and accounted for the Michelson-Morley results.

Pitfalls: theories persist even when disproved by data;
ignoring data inconsistent with dominant paradigm.

In the section called ‘Paradigm and Scientific Revolution’ in this chapter, Jarrard gives a detailed interpretation of Thomas Kuhn’s ideas, yet he dismisses Stephen Toulmin’s arguments by attacking his analogy, and he dismisses alternative opinions with a single reference.

Pitfalls:
ignoring data inconsistent with dominant paradigm;
advocacy masquerading as objectivity;
biased evaluation of subjective data.